The intensity of electric field due to electric dipole physics

The intensity of electric field due to electric dipole

The intensity of the electric field caused by an electric dipole is determined is two situations:

1. Axial or longitudinal position

Consider the electric dipole whose dipole moment is P. The intensity of the electric field at a point P situated at a distance r from the centre of the dipole is to be calculated.

The intensity of electric field at point P due to +q charge
E₁ = [1/4π€0].q/(r+l)²]
Similarly,
The electric field intensity at point P due to -q charge
E₁ = [1/4π€0].q/(r-l)²]
The intensity of resultant electric field at point P.
E = E₂-E₁
E = [1/4π€0].q/(r-l)²]-[1/4π€0].q/(r+l)²]
E = q/4π€0[1/(r-l)²-1/(r+l)²]
E = q/4π€0[{(r+l)²-(r-l)²}/(r²-l²)²]
E = q/4π€0[4rl/(r²-l²)²]
Since,
r >> l
Therefore,
E = q/4π€0[4rl/r⁴]
E = 2/4π€0[2ql/r³]
E= 1/4π€0[2P/r³]
From electric dipole (P=2ql)

2. Axial position of electric dipole

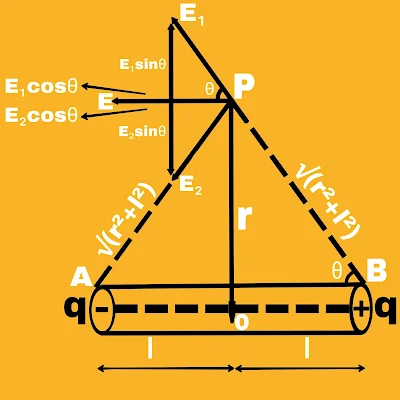
Consider the electric dipole whose dipole moment is P.  From O to the midpoint of the dipole. The electric field at a point P located at a distance is to be calculated in the axisymmetric position.

The intensity of electric field at point P due to +q charge
E₁ = [1/4π€0].q/(r²+l²)] in the direction of PB
Similarly,
The intensity of electric field at the point P due to -q charge
E₂ = [1/4π€0].q/(r²+l²)] in the direction of PA
The intensity of resultant electric field at point P.
E = E₁cosθ + E₂cosθ
E₁ = E₂
E = 2E₁cosθ
E = 2.[1/4π€0].q/(r²+l²)].l/√(r²+l²)
E = [1/4π€0].P/(r²+l²)^3/2
Hense,
l << r
E = [1/4π€0].p/r³

Note

Electric field intensity due to a point charge
E ∝ 1/r²
Electric field intensity due to an electric dipole
E ∝ 1/r³