Distance and Displacement
1. Distance
Suppose an object is along the x-axis. In time t₁ the object reaches A from the original point and in time t₂ the object reaches B from the original point.
AB=(x₂-x₁)=∆x
Duration,
∆t=(t₂-t₁)
Therefore, the length between two points in a given period of time is called distance.
2. Speed
If the distance between two points is ∆x and the time interval between them is ∆t,
Where ∆t=(t₂-t₁)
Therefore, the speed of the object is defined as follows
Speed=Distance/Time
Speed=∆x/∆t
If ∆t=1 second,
Speed = Distance
Therefore, the distance moved by a moving object in specified time is called speed.
Its unit is meter/second. Its dimensions [LT⁻¹].
3. Displacement
It is a vector quantity. When distance is measured keeping the direction in mind, that distance is called displacement. Therefore, the displacement between two points A and B by an object moving along the x-axis,
D=∆x(x₂-x₁)
If x₂>x₁ then ∆x will be positive,
Therefore, on this basis the velocity of the moving object can be calculated.
Velocity=Displacement/Time
If time is 1 second,
Velocity=Displacement
Therefore, the distance displaced by a moving object in unit time is called velocity. The distance displaced represents a direction. Velocity is a vector quantity and its unit is meter/second. Its dimension is [LT⁻¹].
4. Uniform Motion
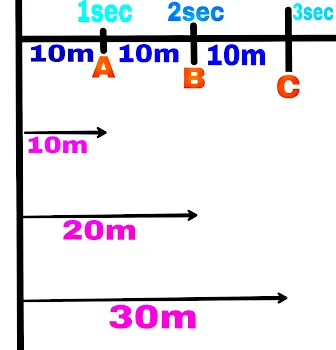
When a moving object covers equal distance in equal time intervals, then the motion of that object is called uniform motion.
5. Non Uniform Motion
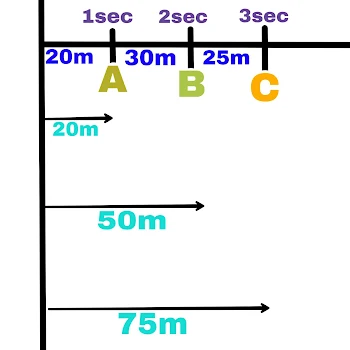
When a moving object covers unequal distances in unequal time intervals, then the motion of that object is called non-uniform motion.
6. Average Speed
The ratio of the total distance traveled by an object in a given period of time and that period of time is called the average speed of the object. It is represented by V.
V=Total distance traveled by the object/Time taken.
If the total distance traveled by an object in time ∆t is ∆s, then
Average speed V=∆s/∆t
7. Instantaneous Movement
It is represented by v and defined mathematically as follows.
Instantaneous speed v=limₓ→₀ ∆s/∆t, (x=∆t)
Or,
ds/dt
Where ds/dt is the differential coefficient of s with respect to t.
Formula for differentiation,
d(xⁿ)/dx=n×n⁻¹
Example-
If the distance of a particle with time is represented by the following equation.
S=2t²+3t
Then find the instantaneous speed of the particle at t=0.
Solution-
S=2t²+3t_____(1)
On differentiating equation (1) with respect to t
ds/dt=4t²⁻¹+3t¹⁻¹
ds/dt=4t+3
ds/dt=4×0+3
ds/dt=3 meter/second
Velocity
If the displacement of an object per unit time is unit, then the velocity of that
object will be 1 meter/sec.
Uniform Velocity
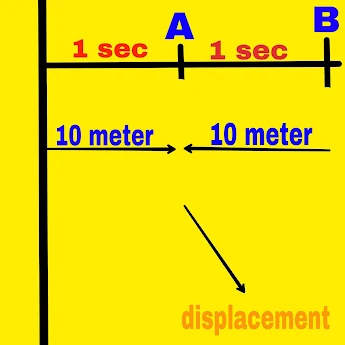
If the displacement of an object is equal in equal intervals of time, then the velocity of the object will be uniform velocity.
Variable Velocity
If the displacement of an object varies in equal time intervals, then in this case the velocity of the object is called changed velocity. The following are the reasons for change in velocity of any object:
1. The result of the velocity of the object changing i.e.,
(a). The value of displacement is changing.
(b). The direction of motion of the object is changing.
2. Both the magnitude and direction of velocity are changing simultaneously.
Average Velocity
The ratio of the total displacement ∆s in a certain time interval ∆t to the time interval ∆t is called the average velocity of the object.
Average velocity (⃗vₐᵥ)=∆s/∆t meter/second
Question- If a person initially walks 3 km towards east and 4 km towards north from the destination and completes his journey, then find out
(a) Total distance traveled by the person
(b).Displacement of person
Solution-

(a).Total distance=3+4=7 km
(b).Displacement OB=√(OA)²+(AB)²
⁼√(9+16)
=√(25)
=5 km
Instantaneous Velocity
The velocity of a moving object on a rod (∆t→0) is called its instantaneous velocity. instantaneous velocity
⃗v=Limₓ→₀∆s/∆t
where x=∆t
⃗v=ds/dt
Difference Between Speed And Velocity
1. The velocity of an object can be positive, negative or zero while the speed of the object can be positive or zero.
2. Velocity is a vector quantity while speed is a scalar quantity and both have the same dimensions.
3. The values of velocity and speed along a straight line will be the same.
4. The ratio of speed and velocity is always greater than one or equal to one.
When velocity and speed are along a straight line, then
speed/velocity=1
If the initial velocity of an object moving with uniform acceleration is u and the final velocity is v, then its average velocity is
⃗V (average)=(⃗u+⃗v)/2
⃗V (average)=(v₁t₁+v₂t₂)/t₁+t₂
Example-
If the velocity of an object in 5 seconds is 10 m/sec and the velocity of the object in 7 seconds is 15 m/sec, then the average velocity of the object is
⃗V (average)=[(10×5)+(15×7)]/7+5
⃗V (average)=155/12
⃗V (average)=12.91 m/s
Acceleration
It is a vector quantity and is defined as follows.
"The rate of change of velocity is called acceleration."
Its dimension is [LT⁻²].
Acceleration=(change in velocity)/time
⃗a=∆⃗v/∆t m/sec²
Uniform Acceleration
If the change in velocity of a moving object is equal in equal time intervals, then the acceleration produced in the object is called uniform acceleration.
Variable Acceleration
If the change in velocity of the object is different in equal time intervals, then the acceleration is called variable or non-uniform acceleration.
Instantaneous Acceleration
The rate of change of velocity of an accelerating particle at any time is called instantaneous acceleration.
a=Limₓ→₀∆v/∆t
where x=∆t,
a=dv/dt
Then,
v=dx/dt
a=(d/dt)×(dx/dt)
a=d²x/dt²
Graphical Representation Of Rectilinear Motion
The graphical representation of rectilinear motion is done in the following relations.
x-t (distance-time) graph
v-t (velocity-time) graph
a-t (acceleration-time) graph
x-t (distance-time) graph
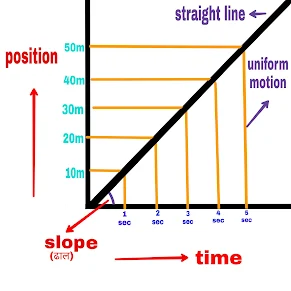
In this graph, time is displayed along the x-axis and various positions of the object are displayed along the y-axis.
The motion of a stationary object, an object moving with a uniform velocity and an object moving with a variable velocity is studied.
1. If the speed of the object is uniform
The graph will be a straight line.
The slope of the straight line tells the particles and their average speed.
The average velocity of the particle is equal to the instantaneous velocity.
2. If the speed of the object changes
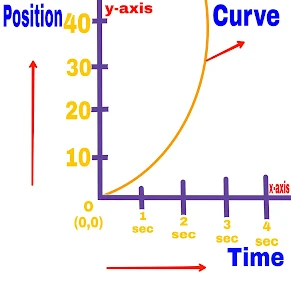
In this situation the velocity of the object changes with time.
In this situation the graph drawn will be a curve whose slope will be different in different intervals.
The average velocity and instantaneous velocity of the particle are different.
3. Displacement Of Object With Time under Different Circumstances
(a).

In this situation the object is at rest.
(b).
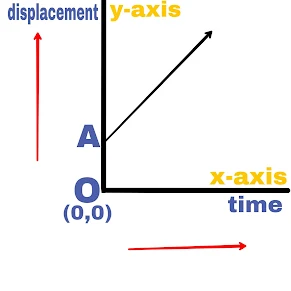
The slope of the time displacement graph is positive. Hence the object is move with a constant velocity.
(c).
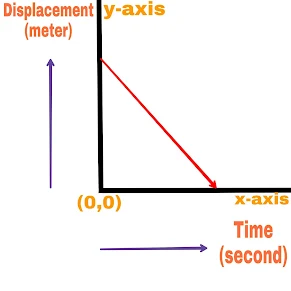
The slope of the time displacement graph is negative and constant and the object is moving with a constant negative velocity.
(d).
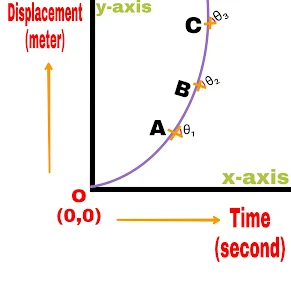
The slope of the time displacement graph is different at different points. But it is increasing with time.
(e).
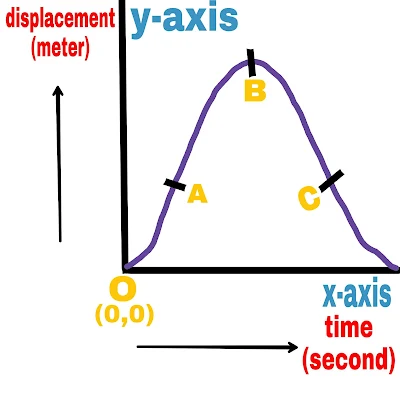
The slope of the time displacement graph is changing with time.
The velocity of the object is increasing at O-A.
The velocity of the object is decreasing at A-B.
The velocity of the object at B is zero.
The velocity of the object at B-C is negative.
v-t (velocity-time) graph
With the help of this graph, we measure the velocity of a moving object at
different time intervals and draw a graph with time.
Velocity is drawn along the y-axis and time along the x-axis.
1. If the object moves with uniform velocity

The velocity time graph will be a straight line parallel to x-axis.
The velocity time graph and the area of the region bounded by the time axis express the distance traveled by the object in a given time interval.
Therefore, in the above graph, the distance traveled by the object in the time interval (t₂-t₁),
S=v(t₂-t₁)
S=Area of rectangle BC(t₂-t₁)
2. If the velocity of the object is increasing at a uniform speed

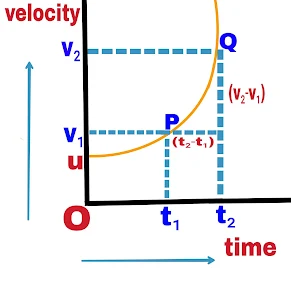
(a). The slope of the velocity time graph represents the acceleration of the object. The velocity of the object at point A of the straight line is v₁ and the velocity of the object at another point C is v₂.
Therefore, the change in velocity of the object in the time difference (t₂-t₁) is (v₂-v₁).
Hence the acceleration of the object,
a = BC/AB
a=(v₂-v₁)/(t₂-t₁)
a=∆v/∆t
(b). If the object is moving with uniform velocity then its average acceleration and instantaneous acceleration will be equal.
Average Acceleration = Instantaneous Acceleration
∆v/∆t=dv/dt
3. If object is moving with variable velocity
In this situation, to find the slope of the object at points P and Q, the change in velocity corresponding to straight line PQ is (v₂-v₁) and time interval (t₂-t₁)=∆t,
average speed,
⃗a=∆v/∆t
and instantaneous acceleration,
⃗a=Limₓ→₀∆v/∆t
where x=∆t
⃗a=dv/dt
a-t (acceleration-time) graph
1. If the particle is at rest

If the particle is at rest, then the velocity and acceleration of the particle at rest is zero. Hence the graph will be superimposed on the time axis.
2. If the object moves with a constant velocity
In other words,
Acceleration = zero

In this case the graph will be represented on the time axis only.
3. If the object moves with a constant acceleration
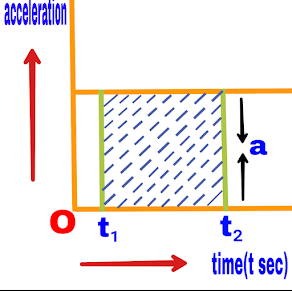
If an object moves with a constant acceleration, the time acceleration graph will appear as follows.
With the help of this graph, the change in velocity ∆v of a moving object between any two time intervals t₁ and t₂ can be calculated.
a=(velocity change)/time
a=∆v/∆t
∆v=a.∆t meter/second
Equation of motion with the help of graph method
When a particle is moving with uniform acceleration along a straight line, then the mathematical equation by which the relationships of the quantities like velocity, acceleration, displacement etc. of such particle are expressed is called the equation of motion of the object.
The following equations of motion are
v=u+at
s=ut+at²/2
v²=u²+2as
Deduction of equations of motion with the help of graphical method
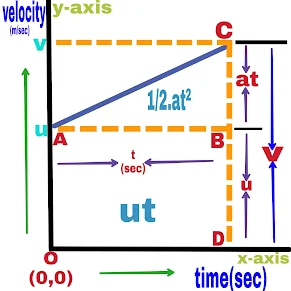
1. Velocity-Time Relation (v=u+at)
With the help of the above graph,
Suppose an object is move with uniform acceleration a. Its initial velocity is u(t=0), after time t the velocity of the particle becomes v.
Slope of straight line AC
Acceleration=Perpendicular/Base
a=BC/AB
a=(v-u)/t
at=v-u
v=u+at
2. Position-Time Relation (s=ut+at²/2)
With the help of the above graph,
distance traveled by a moving object
s=area enclosed between velocity time graph and the time axis
s=∆ABC+Area of ABDO
s=1/2×(AB×BC)+(AB×BD)
s=1/2.t(v-u)+t×u
s=1/2.t(at)+ut
s=1/2.at²+ut
s=ut+1/2.at²
3. Position-Velocity Relation (v²=u²+2as)
With the help of the above graph,
Distance traveled by a moving object at any instant t
s=(sum of parallel sides × distance between them)/2
s=[(AO+CD)×OD]/2
s=[(u+v)×t]/2
From relation (1)
v=u+at
t=(v-u)/a
s=[(u+v)×(v-u)/a]/2
s=(v²-u²)/2a
v²=u²+2as
Motion under gravity acceleration
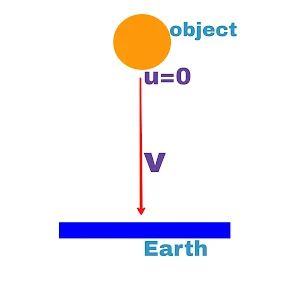
When the object is released from a height h rest independently of the position
If the velocity of the particle after time t is v, then
Equation of the motion will be as follows:
1. v=u+gt
v=0+gt
v=gt
2. h=ut+1/2.gt²
h=0+1/2.gt²
h=1/2.gt²
3. v²=u²+2gh
v²=0+2gh
v²=2gh
v=√(2gh)
0 Comments
Post a Comment